Proceso y propuesta de modelos de distritación electoral federal en México: Criterios, algoritmos y geolocalización
Descripción del marco legal, criterios de asignación y modelos matemáticos para la delimitación de los 300 distritos electorales federales en México, incluyendo optimización entera y clusterización geográfica.
Autoría: Isabel Quintas Pereira
Abstract
La distritación electoral federal en México se fundamenta en la Reforma de 1977, que estableció 300 distritos uninominales y 200 plurinominales para equilibrar la representación política. Cada redistribución (1996, 2005, 2017 y 2022) responde a los censos decenales y a criterios de homogeneidad poblacional y compactación geográfica, garantizando al menos dos distritos por entidad y la proximidad en tiempos de traslado.
El proceso de asignación del número de distritos por estado se modela como un problema de optimización entera: se busca minimizar la desviación de la población real frente a la población ideal de 420,000 habitantes por distrito. Mediante variables binarias y restricciones de suma ![]() , se decide a 15 estados ubicados dónde recibirán un distrito extra, logrando una desviación promedio inferior al 5 %. Herramientas como Excel Solver o software de programación lineal son útiles para resolverlo.
, se decide a 15 estados ubicados dónde recibirán un distrito extra, logrando una desviación promedio inferior al 5 %. Herramientas como Excel Solver o software de programación lineal son útiles para resolverlo.
Para la delimitación geográfica interna de cada estado, se emplea un enfoque de clustering (K-medias) adaptado a restricciones legales (secciones de 100–3 000 electores) y logísticas (ubicación de casillas, cabeceras municipales). El modelo define variables binarias ![]() que asignan municipios a centroides distritales, sujeta a límites de población empadronada y criterios de compacidad y cercanía. Este planteamiento garantiza distritos equilibrados tanto numéricamente como geográficamente.
que asignan municipios a centroides distritales, sujeta a límites de población empadronada y criterios de compacidad y cercanía. Este planteamiento garantiza distritos equilibrados tanto numéricamente como geográficamente.
A consecuencia de la Reforma Electoral de 1977, se estableció que la cantidad de distritos electorales, a los cuales les corresponde un representante uninominal en la Cámara de Diputados es de 300 distritos.
La subdivisión del país en estas 300 unidades se realiza tomando en cuenta el número de habitantes que indica el último censo nacional ya que los diputados representan los intereses de la población. Además la reforma de 1977 establece el número de 200 diputados plurinominales con el propósito de equilibrar las preferencias políticas de los habitantes, ya que se nombran tomando en cuenta la proporción de votantes de los distintos partidos.
Debido al aumento de la población y a las modificaciones de estos sobre el territorio es necesario redefinir los distritos cada vez que los censos decadales indiquen cambios nen la distribución de la
población.
Para realizar la delimitación geográfica de estos 300 territorios deben tomarse en cuenta ciertos
criterios básicos:
- Que el número de ciudadanos sea lo más parecido posible en cada distrito.
- Que cada distrito pertenezca a una sola entidad federativa.
- Que ningún estado tenga menos de dos distritos, independientemente de su población.
- Que los distritos sean geográficamente compactos.
- Que las poblaciones que los conforman sean cercanas en tiempo de traslado (no en kilómetros)
Dado que el número de habitantes se ha duplicado desde 1977 cuando éramos cercano a los sesenta millones de habitantes y ya superamos los 120 millones, los distritos electorales han tenido que redefinirse cambiando la geografía electoral. Se produjeron modificaciones en 1996, en 2005, 2017 y el último en 2022, de acuerdo a los datos del censo del 2020.
Figura 1: Evolución de la población en México
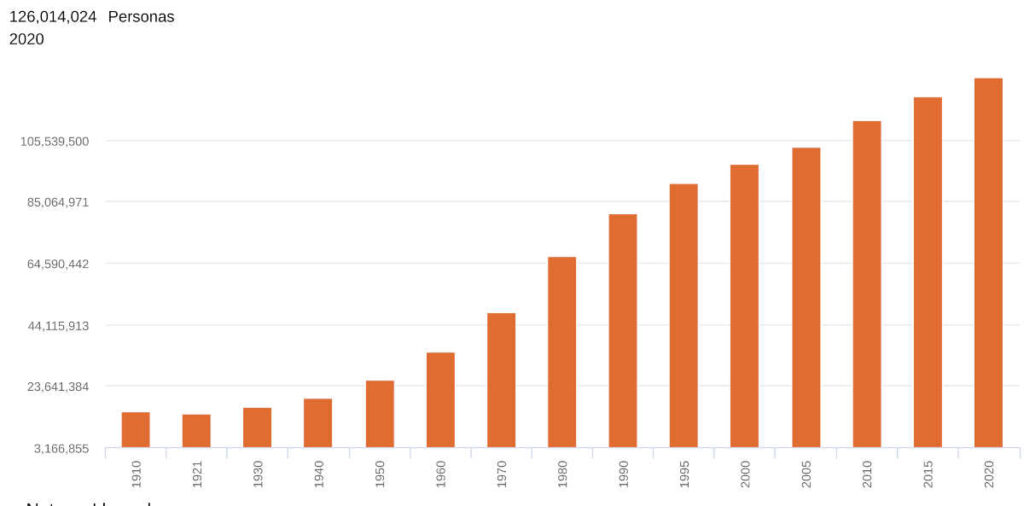
Fuente: Instituto Nacional de Estadística y Geografía (INEGI)
El censo del año 2020 contabiliza aproximadamente 126 millones de habitantes; dado que esta población estará representada por 300 diputados, cada uno de los 300 distritos debería tener una población cercana a la población total dividida entre 300, o sea ![]() individuos.
individuos.
Como a cada distrito debería corresponder cantidades equivalentes de población, los 126 millones deberían ser divididos entre los 300 distritos, correspondiendo entonces a 420,000 habitantes por distrito.
Llamaremos a este valor Población equitativa: ![]()
Esto no se puede lograr perfectamente, habrá que distribuirlos tomando en cuenta los diferentes criterios. En la cuarta columna del Cuadro 2 se muestra el número de representantes que le correspondería a cada estado de manera proporcional a su población. En primer lugar el número de distritos debe ser un número entero, además se establece que ningún estado tendrá menos de dos distritos electorales lo que obliga a asignar los estados de Colima y de Baja California Sur en dos distritos para cada estado
El problema que se presenta es un problema de índole político ya que determinar el número de
distritos electorales es definir cuantos diputados le corresponden a cada estado. La segunda parte
del problema es determinar la partición geográfica que le corresponderá a cada distrito,
balanceando la cantidad de población de cada uno de ellos sujetos a ciertas restricciones
particulares.
Determinación del número de distritos de cada entidad federativa
Es necesario ahora determinar cuantos distritos debe tener cada uno de los estados pero del cálculo previo solo quedan determinados cuatro estados:
- Colima: 2 distritos
- Baja California Sur: 2 distritos
por la restricción que indica que al menos debe haber dos distritos por estado y otros dos cuya población se ajusta aproximadamente a un múltiplo de la población ideal por distrito:
- Sonora: 7 distritos
- Baja California Norte: 9 distritos
Para los otros 28 estados, el cálculo previo indica el número mínimo de distritos, que sumados con los anteriores nos da 285 distritos. Como la ley indica que deben ser 300 distritos electorales en total y como cada distrito debe estar contenido en un solo estado, es necesario asignar los otros 15 distritos a algunos de los 28 estados restantes.
Para esta asignación se utilizará el criterio de que el número de habitantes de cada uno de los distritos sea lo más homogéneo posible, o sea que la población del distrito difiera lo menos posible del número calculado de 420,047 individuos. Se analizarán un par de estados para entender el problema, en particular un estado con mucha población y otro con escasa población: el Estado de México y Tlaxcala, por ejemplo.
Estado de México
La población de Estado de México según el censo fue de 16,992,400 personas y como a cada distrito le corresponderían 420,047, al dividir la población entre este número se obtiene 40.5, por lo que habrá que decidir si se le asignan 40 o 41 distritos.
Veamos que población tendía cada distrito si se divide en 40 o en 41 y muy importante, cual sería la diferencia respecto a la distribución ideal:
| Población | Diferencia respecto a distribución ideal |
| |
| |
O sea que si se divide en 40 distritos, cada uno tendría aproximadamente 4,760 individuos de más pero si se divide en 41 distritos, cada uno tendría aproximadamente 5,600 individuos menos.
Tlaxcala
Ahora haremos el mismo análisis para un estado pequeño como es Tlaxcala con solo 1,343,000 habitantes. Dividiendo su población entre en número promedio de habitantes que debería tener cada distrito resulta 3.2, por lo que habrá que dividirla en 3 o en 4 distritos. Haremos el mismo cálculo:
| Población | Diferencia respecto a distribución ideal |
| |
| |
Una primera observación que se puede hacer es que en el estado al que se le asignarían 40 o 41 distritos la variación en el número de individuos por distrito variaría entre el 1% al 1.5% de la población equitativa, mientras que en el caso del estado donde la variación es de 3 o 4 distritos la variación de la población es mucho mayor llegando casi al 20%. Esto posiblemente dejará en desventaja a los estados poco poblados para lograr una mayor representación.
En las columnas 5 y 6 de la tabla An se muestran los valores calculados de las diferencias en exceso si se asignan n distritos y las cantidades en defecto si se asignaran n + 1 distritos a cada uno de los estados en que no queda determinado exactamente en número de distritos.
Si el único criterio es que la población resultante en los distritos de cada estado difiera lo menos posible respecto de la población equivalente Pe de 420,000 y como de los 300 distritos ya quedaron definidos 285, hay 15 distritos a repartir entre los 28 estados, se puede plantear como un problema de optimización entera, donde se le asignará 1 distrito más a solo 15 estados.
Cuadro 1: Número de distritos por entidad federativa usando optimización entera
| Entidad federativa | Población | % población | N° inicial distritos | de más | de menos | N° de distritos |
| Estado de México (15) | 16,992,400 | 13.5 | 40.5 | 4,763 | -5,598 | 40 |
| CDMX (9) | 9,209,900 | 7.3 | 21.9 | 18,520 | -1,415 | 22 |
| Jalisco (14) | 8,348,150 | 6.6 | 19.9 | 19,329 | -2,640 | 20 |
| Veracruz (30) | 8,062,600 | 6.4 | 19.2 | 4,300 | -16,917 | 19 |
| Puebla (21) | 6,583,300 | 5.2 | 15.7 | 18,840 | -8,591 | 16 |
| Guanajuato (11) | 6,166,900 | 4.9 | 14.7 | 20,446 | -8,920 | 15 |
| Nuevo León (19) | 5,784,450 | 4.6 | 13.8 | 24,911 | -6,872 | 14 |
| Chiapas (7) | 5,543,800 | 4.4 | 13.2 | 6,399 | -24,061 | 13 |
| Michoacán (16) | 4,748,850 | 3.8 | 11.3 | 11,667 | -24,310 | 11 |
| Oaxaca (20) | 4,132,150 | 3.3 | 9.8 | 39,081 | -6,832 | 10 |
| Baja California (2) | 3,769,000 | 3 | 9 | – | – | 9 |
| Chihuahua (8) | 3,741,870 | 3 | 8.9 | 47,687 | -4,284 | 9 |
| Guerrero (12) | 3,540,700 | 2.8 | 8.4 | 22,541 | -26,636 | 8 |
| Tamaulipas (28) | 3,527,700 | 2.8 | 8.4 | 20,916 | -28,080 | 8 |
| Coahuila (5) | 3,146,750 | 2.5 | 7.5 | 29,489 | -26,703 | 8 |
| Hidalgo (13) | 3,082,850 | 2.4 | 7.3 | 20,360 | -34,691 | 7 |
| Sinaloa (25) | 3,026,950 | 2.4 | 7.2 | 12,374 | -41,678 | 7 |
| Sonora (26) | 2,944,850 | 2.3 | 7 | – | – | 7 |
| San Luis Potosí (24) | 2,822,250 | 2.2 | 6.7 | 50,328 | -16,868 | 7 |
| Tabasco (27) | 2,402,600 | 1.9 | 5.7 | 60,473 | -19,614 | 6 |
| Querétaro (22) | 2,368,450 | 1.9 | 5.6 | 53,643 | -25,305 | 6 |
| Yucatán (31) | 2,320,900 | 1.8 | 5.5 | 44,133 | -33,230 | 6 |
| Morelos (17) | 1,971,500 | 1.6 | 4.7 | 72,828 | -25,747 | 5 |
| Quintana Roo (23) | 1,858,000 | 1.5 | 4.4 | 44,453 | -48,447 | 5 |
| Durango (10) | 1,832,650 | 1.5 | 4.4 | 38,116 | -53,517 | 4 |
| Zacatecas (32) | 1,622,100 | 1.3 | 3.9 | 120,653 | -14,522 | 4 |
| Aguascalientes (1) | 1,425,800 | 1.1 | 3.4 | 55,220 | -63,597 | 3 |
| Tlaxcala (29) | 1,343,000 | 1.1 | 3.2 | 27,620 | -84,297 | 3 |
| Nayarit (18) | 1,235,450 | 1 | 2.9 | 197,678 | -8,230 | 3 |
| Campeche (4) | 928,350 | 0.7 | 2.2 | 44,128 | -110,597 | 2 |
| Baja California Sur (3) | 798,450 | 0.6 | 1.9 | – | – | 2 |
| Colima (6) | 731,400 | 0.6 | 1.7 | – | – | 2 |
| Total | 126,014,070 | 100 | 100 | 300 | – | 300 |
Volvamos a analizar los datos de los dos estados calculados. Para el estado de México la población por distrito variaría de ![]() si se le asignan 41 ó 40 distritos electorales, mientras que para el estado de Tlaxcala esta variación sería mucho mayor, de
si se le asignan 41 ó 40 distritos electorales, mientras que para el estado de Tlaxcala esta variación sería mucho mayor, de ![]() . Se observa que para Tlaxcala tanto con 3 como con 4 distritos se encuentra lejos de la población promedio. SI el único criterio es disminuir estas diferencias, se puede pensar es escoger los estados de tal manera que la suma de las diferencias sea la menor posible; esto nos lleva a un problema de optimización, queremos minimizar la suma de las diferencias.
. Se observa que para Tlaxcala tanto con 3 como con 4 distritos se encuentra lejos de la población promedio. SI el único criterio es disminuir estas diferencias, se puede pensar es escoger los estados de tal manera que la suma de las diferencias sea la menor posible; esto nos lleva a un problema de optimización, queremos minimizar la suma de las diferencias.
Las variables serán las diferencias, llamaremos ![]() al exceso de población del estado
al exceso de población del estado ![]() cuando se le asignan
cuando se le asignan ![]() distritos y
distritos y ![]() al faltante de población del estado
al faltante de población del estado ![]() si se le asignan
si se le asignan ![]() distritos.
distritos.
El modelo se puede ver de la siguiente manera:
![Rendered by QuickLaTeX.com \[ Min \sum_{1}^{28} a_i \Delta_{+i} - \sum_{1}^{28} b_i \Delta_{-i} \]](https://economia.xoc.uam.mx/contenido/ql-cache/quicklatex.com-1f51f2df5edbca6d15ccd88c20fd2366_l3.png)
Donde ![]() y
y ![]() toman los valores
toman los valores ![]()
sea
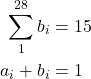
para todo ![]()
Por lo tanto se trata de un problema de optimización entera, minimización en este caso,
que tiene 56 variables y 29 restricciones.
Claro que se podrían agregar otras consideraciones de orden político o social, que tal vez
añadirían restricciones. Par el propósito de este material desarrollaremos las ecuaciones
del problema planteado:
![]()
Sujeto a:
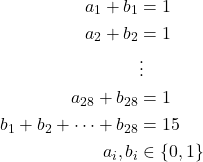
El problema se resuelve utilizando algún software de programación lineal con programación entera. Se
puede utilizar la utilería solver de Excel indicando que las 56 variables son de tipo
binario, con lo cual el sistema lo resolverá como un problema de programación entera.
La solución obtenida indica que los estados que tendrán un distrito, y por ende un diputado más son 1: CDMX, 2: Jalisco, 3: Puebla, 4: Guanajuato, 5: Nuevo León, 6: Oaxaca, 7: Chihuahua, 8: Coahuila, 9: San Luis potosí, 10: Tabasco, 11: Querétaro, 12: Yucatán, 13: Morelos, 14: Zacatecas, 15: Nayarit. En la última columna del cuadro A1 se muestra el número de distritos asignados a cada estado. Esta selección indica una desviación promedio de 18 mil habitantes por estado, menor al 5% de la población esperada.
Geolocalización de los sectores dentro de cada distrito electoral
El cálculo previo permitió determinar el número de distritos y por ende el número de representantes ante el congreso para cada una de las 32 entidades federativas del país. El paso siguiente es la determinación geográfica de cada uno de los distritos. Esta etapa del trabajo es más compleja porque no solo se trata de un cálculo numérico sino que se debe tomar en cuenta, además de la legislación, la distribución espacial geográfica de la población.
La Ley general de Instituciones y Procedimientos Electorales, conocida como la LGIPE¹ , en el artículo 147 establece que cada sección electoral tendrá un mínimo de 100 y un máximo de 3,000 electores. Lo primero a destacar es que para los sectores no se está tomando en cuenta a la población general sino solamente a los electores potenciales dados de alta en el padrón electoral unos pocos meses antes de la elección correspondiente; también es importante destacar que además de los criterios federales, los estados suelen tener leyes y reglamentaciones propias para la representación estatal. Dentro de cada sección se tendrán que abrir casillas electorales donde votarán los ciudadanos. En cada sección se abrirá de una a cuatro casillas ya que a cada una se le pueden asignar hasta 750 votantes. En estos casos habrá una principal y las complementarias.
Los datos de los que se dispone son:
- El número de distritos a crear
- La población inscrita en el padrón
- Las poblaciones urbanas y rurales donde se deben instalar las casillas de votación
- La georreferenciación de los centros de votación
La distribución tiene que seguir algunos criterios como:
- En cada distrito debe haber una cantidad similar de votantes
- Los distritos deben ser compactos
- Se debe procurar que las distancias, medidas en kilómetros o tiempo de traslado, sean las menores posibles dentro del distrito.
Para realizar esto el Instituto Nacional Electoral (INE) debe tomar en cuenta que dentro del estado hay poblaciones de distintos tamaños agrupadas en municipios, cada uno de ellos con una cabecera municipal donde se asientan las oficinas de las distintas instancias; en cada población con más de 100 individuos con capacidad de voto se deberá instalar una casilla. Cada una de estas casillas debe ser asignada a alguno de los distritos electorales; en el estado existirán N de estos puntos, cada uno de los cuales tiene al menos 3 valores asociados: xi, yi, correspondientes a su posición geográfica y vi la cantidad de votantes; este punto debe ser asignado a alguno de los K distritos del estado.
Tenemos un gran número de puntos N, que debemos agrupar en un número restringido K de grupos tratando de que se cumplan los tres criterios anteriores: Compactos, similares en número de electores y cercanos.
Uno de los métodos más empleados para el caso de agrupar un gran número de datos es el conocido como el de las K- medias, también conocido como método de cluster.
Algoritmo del método de clusterización/k-medias
El método de las K-medias es un método iterativo donde se tienen ![]() puntos o elementos que se quieren agrupar en
puntos o elementos que se quieren agrupar en ![]() grupos de tal manera que las diferencias (distancias) dentro del grupo sean las menores posibles según alguna de sus características, respecto al centro.
grupos de tal manera que las diferencias (distancias) dentro del grupo sean las menores posibles según alguna de sus características, respecto al centro.
Supongamos que tememos un conjunto de ![]() puntos en un espacio, del que conocemos la posición
puntos en un espacio, del que conocemos la posición ![]() de cada punto y queremos agrupar estos
de cada punto y queremos agrupar estos ![]() puntos en
puntos en ![]() grupos, de tal manera que se minimicen las distancias entre estos puntos al centro del grupo, denominado el centroide. Pero el centro del grupo es algún punto de este espacio
grupos, de tal manera que se minimicen las distancias entre estos puntos al centro del grupo, denominado el centroide. Pero el centro del grupo es algún punto de este espacio ![]() desconocido. Definiremos la distancias como
desconocido. Definiremos la distancias como ![]() :
:
![]() : Distancia del punto
: Distancia del punto ![]() al centro del grupo
al centro del grupo ![]()
El algoritmo trata de asignar cada punto al centroide del grupo ![]() más cercano, pero como inicialmente no se conoce donde están los centroides, se asignan arbitrariamente o bajo algún criterio previo, para luego asignar los puntos a cada grupo de tal manera que la distancia sea mínima.
más cercano, pero como inicialmente no se conoce donde están los centroides, se asignan arbitrariamente o bajo algún criterio previo, para luego asignar los puntos a cada grupo de tal manera que la distancia sea mínima.
![]() para
para ![]()
Terminados de asignar los ![]() puntos a alguno de los
puntos a alguno de los ![]() grupos se recalcula el centroide de cada grupo
grupos se recalcula el centroide de cada grupo ![]()
Y se repite el paso anterior volviendo a asignar los ![]() puntos a estos nuevos
puntos a estos nuevos ![]() centroides. El proceso se repite hasta que no haya más cambios o hasta tener una distribución satisfactoria.
centroides. El proceso se repite hasta que no haya más cambios o hasta tener una distribución satisfactoria.
Entonces los pasos del algoritmo serán:
- Se definen los
 centroides
centroides - Se asigna cada punto al centroide más próximo
- Se recalcula el centroide
- Se repite el paso 2 y 3
En las gráficas siguientes se muestra a) el espacio con N puntos; en b) se asignan arbitrariamente 3 centroides y se muestra para dos puntos la distancia euclidiana a estos tres centros, lo que permite determinar a cual están más cerca y a ese serán asignados; en el siguiente gráfico se muestra como quedaros los grupos en esta primera iteración, para finalmente volver a calcular los centroides y repetir el proceso de asignación a estos; si no hay cambios esa será la mejor distribución, en caso contrario se repite.
Figura 2: Clusterización distrital
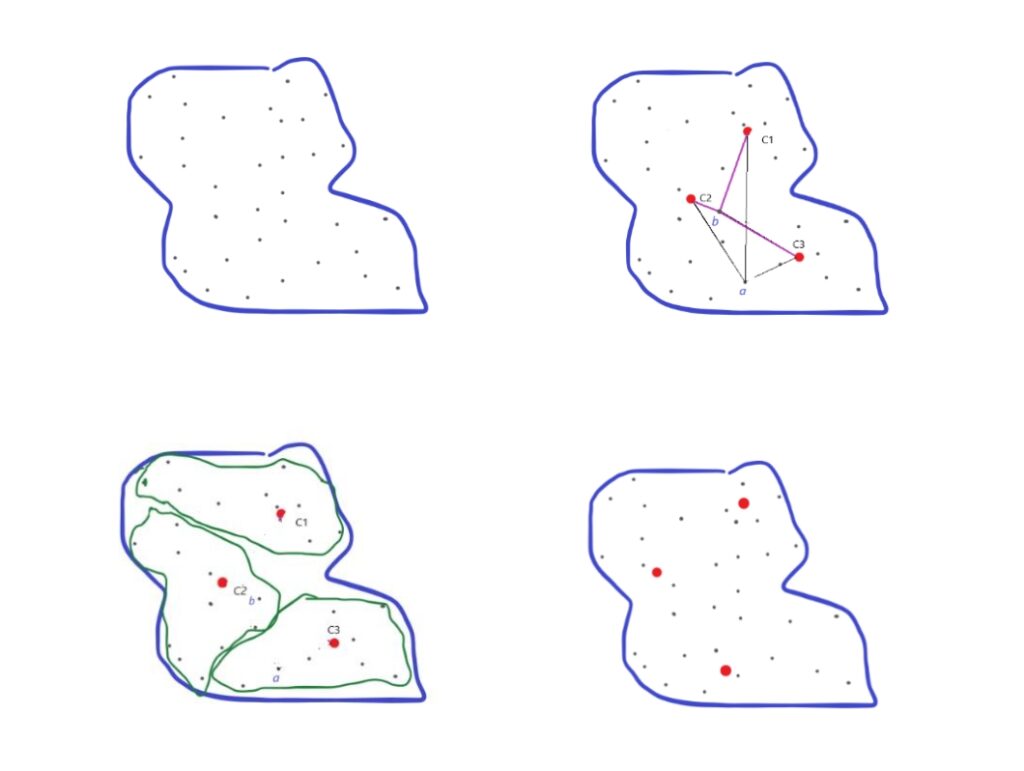
Fuente: elaboración propia.
a) se tiene un conjunto de puntos; b) centros arbitrarios y distancias a estos centros; c) se establecen los grupos y d) se recalcula la posición de los centros.
Este problema también se puede tratar como un problema de programación lineal, donde se quiere minimizar la suma de las distancias a los centroides y las variables son las coordenadas de los puntos y la asignación de cada punto a los respectivos centros.
Sin embargo el algoritmo de agrupamientos por el método de las K-medias es sensible a los puntos iniciales que se asigna a los centroides y además el número de elementos de cada grupo puede ser muy diferente, por lo que es necesario adaptarlo para realizar la distribución territorial en el caso de los distritos electorales. Otro inconveniente es que el tiempo de resolución aumenta exponencialmente con el número de puntos.
El problema de la definición territorial de los distritos electorales
En México la división política del territorio la constituyen 32 estados que a su vez se dividen en municipios y en el caso de la ciudad de México en alcaldías. Los municipios a su vez se clasifican en urbanos, semiurbanos u rurales dependiendo del tamaño de las poblaciones que se encuentran en su territorio y el tipo de actividades predominantes.
Dado el tamaño de los estados, casi todos con varios millones de habitantes, donde más del 60% está empadronado, el número de secciones o casillas electorales sería demasiado grande para aplicar el modelo matemático.
Hay ciertos criterios que se utilizan para la determinación territorial de los distritos electorales:
- Cada municipio debe estar totalmente contenido en un distrito electoral.
- En número de electores de cada distrito no debe diferir más que un pequeñoporcentaje de los otros distritos.
- Deben se compactos en lo posible.
- Se utilizan las coordenadas de las cabeceras municipales como puntos representativos de estas.
- El centro del distrito electoral corresponderá a alguna cabeza municipal importante.
Para definir el modelo se condiera:
- A cada punto
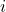 se le asocian tres parámetros
se le asocian tres parámetros  , las coordenadas geográficas de la cabecera municipal y el número de empadronados en el municipio.
, las coordenadas geográficas de la cabecera municipal y el número de empadronados en el municipio. - La distancia será la distancia geométrica entre las dos cabeceras a considerar
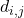 donde
donde 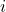 varía de
varía de 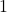 a
a 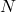 y
y 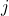 corresponde al centro del distrito de
corresponde al centro del distrito de 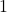 a
a 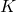 .
. - La variable a considerar es la pertenencia o no de un punto
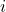 al distrito
al distrito 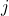 y se llamará
y se llamará 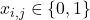 .
. - Se considerará
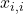 al centroide del distrito
al centroide del distrito 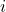 .
. - El porcentaje de variación de la población empadronada respecto de la media es
Entonces, el modelo queda de la siguiente forma:
![Rendered by QuickLaTeX.com \[ Min \sum_{1}^{N} \sum_{1}^{K} d_{i,j} x_{i,j} \]](https://economia.xoc.uam.mx/contenido/ql-cache/quicklatex.com-452fe1a8f8edf936f029e453c22812df_l3.png)
Sujeto a:
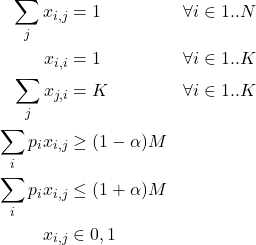
Donde ![]() es la población media empadronada de los distritos del estado.
es la población media empadronada de los distritos del estado.
La primera restricción garantiza que cada municipio pertenezca a un solo distrito; la segunda restricción garantiza que el municipio central pertenezca al distrito; las restricciones 4 y 5 establecen los límites de la población empadronada en cada distrito.
El planteamiento del problema ahora es conocido en número de distritos que debe tener un estado, y con la información ofrecida por las Juntas Locales sobre los ciudadanos de cada localidad inscriptos en el padrón electoral, es necesario determinar la partición geográfica del territorio del estado en los distritos electorales.
Los datos de que se dispone son:
- El número de distritos a crear
- La población inscrita en el padrón
- Las poblaciones rurales y urbanas donde se deben instalar las casillas de votación
- La georreferenciación de los centros de votación
La distribución tiene que seguir algunos criterios como:
- Los distritos deben ser compactos
- Deben cubrir todo el estado
- Deben tener aproximadamente el mismo número de votantes
Análisis del modelo para un estado: Morelos
El estado de Morelos tiene una población cercana a los 2 millones de personas, los que se distribuyen en cerca de 1,400 poblaciones rurales y otras 350 urbanas. La población empadronada para la elección del 2024 es de 1 millón 370 mil personas , el 65% aproximadamente, distribuidos en 907 secciones electorales donde se instalarán 2,324 casillas. Para la organización administrativa se organiza en 33 municipios.
Aplicar el modelo anterior a las poblaciones o a las secciones electorales para el tamaño del estado es un problema matemáticamente muy difícil y no garantizaría que todos los poblados de un municipio quedaran en el mismo distrito, por lo que se tratará de asignar los 33 municipios a alguno de los 5 distritos electorales federales.
La información necesaria serán las coordenadas geográficas de las cabeceras municipales que se pueden obtener del INEGI y el número de votantes que aparece en el padrón electoral del INE e IMPEPAC².
Con estas restricciones el modelo de distritación queda de la siguiente forma:
- El número de variables
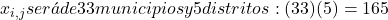
- Se deben calcular las 165 distancias entre los puntos
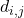
- La función objetivo tendrá 165 sumandos
![Rendered by QuickLaTeX.com \[ Min \sum_{1}^{N} \sum_{1}^{K} d_{i,j} x_{i,j} \]](https://economia.xoc.uam.mx/contenido/ql-cache/quicklatex.com-452fe1a8f8edf936f029e453c22812df_l3.png)
Sujeto a (la restricción se tiene que escribir para cada distrito):
![]()
La siguiente restricción también tendrá que escribirse 5 veces; así como se presenta presupone que inicialmente se colocaron en los 5 primeros lugares las cabezas de distrito. Si no fuera así habrá que agregar condiciones que recalculen los centroides.
![]()
De igual manera las siguientes restricciones que exigen que la población empadronada en cada distrito no varíe en más o menos que 20% respecto a la número de empadronados del estado entre 5 debe escribirse para cada distrito.
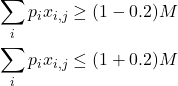
En total, el problema se reduce a un PL entero con 165 variables y 20 restricciones xon ![]()
En la siguiente figura se muestra distribución geográfica de los distritos electorales como los presentas el INE. Los distritos más urbanos son el distrito 1 correspondiente a Cuernavaca, la capital del estado y el distrito 2 correspondiente a 4 municipios conurbanos con Cuernavaca.
Figura 3: Distritación en Morelos 2022
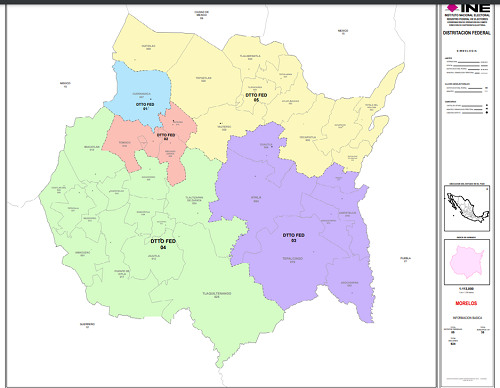
Fuente: Instituto Nacional Electoral (INE)
Notas al pie de página:
¹ En cumplimiento del artículo 147, párrafo 3, de la Ley General de Instituciones y Procedimientos Electorales (LGIPE), que establece que cada sección tendrá como mínimo 100 y como máximo 3,000 electores, la Dirección Ejecutiva del Registro Federal de Electores (DERFE), a través de la Dirección de Cartografía Electoral y de las Juntas Locales y Distritales Ejecutivas (JLE y JDE), efectúa el programa de integración seccional a fin de configurar secciones con el rango de electores que corresponda.
² Instituto Morelense de Procesos Electorales y participación Ciudadana
Bibliografía
Martínez Ttamues, Pastora F., 2012, Diseño de Circunscripciones Electorales en el Ecuador; tesis Escuela Politécnica nacional, Facultad de Ciencias , Ecuador.
Datos obtenidos de:
INE, https://central electoral.ine.mx/2022/
IMPEPAC, https://impepac.mx/distritacion-electoral-local-para-morelos





